

Next: optimize
Up: Namelist Command Dictionary
Previous: matrix_output
- type: action command.
- function: determine momentum aperture as a function of position in the lattice by tracking
&momentum_aperture
STRING output = NULL;
double x_initial = 0;
double y_initial = 0;
double delta_negative_start = -0.10;
double delta_positive_start = 0.10;
long delta_step_size = 0.01;
long oversteps = 1;
long splits = 2;
long steps_back = 4;
double s_start = 0;
double s_end = DBL_MAX;
STRING include_name_pattern = NULL;
long verbosity = 0;
&end
output -- The (incomplete) name of a file to which the momentum aperture results will be written.
Recommended value: ``%s.mmap''.
x_initial, y_initial -- The initial x and y coordinate values for tracking. It is essential
that y_initial be nonzero if one wants to see losses due to vertical resonances.
delta_negative_start, delta_positive_start --
Start values of scans in the negative and positive
directions. Scanning begins at these and moves toward 0.
delta_step_size -- Initial size of steps in 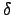 . This should
be fairly large in order to save time.
. This should
be fairly large in order to save time.
oversteps -- Number of step sizes to go past the point of first
survival before reversing the direction of scanning.
splits -- Number of times to split the step size in
order to refine the location of the maximum surviving momentum
offsets. When a particle is lost, the algorithm steps back to a momentum offset
where a particle survived, subdivides the step size, and continues searching.
steps_back -- When performing interval splitting, when a particle is
lost, the algorithm steps back to a momentum offset where a particle survived.
This method helps to ensure that the algorithm did not find a stable island.
This is the number of steps to go back.
s_start, s_end -- Limiting s coordinates of the
elements from which tracking will start. The default values will
exclude no elements.
include_name_pattern -- If given, tracking will start
only at the entrance to elements that match the given wildcard
pattern.
verbosity -- Larger values result in more detailed
printouts as calculations proceed. Mostly for debugging.
The idea for this command is from M. Belgroune et al., ``Refined
Tracking Procedure for the SOLEIL Energy Acceptance Calculation,''
Proceedings of PAC 2003, p 896, as implemented for TRACYII. In
particular, the energy aperture as a function of position around the
ring is determined by tracking. Starting at the beginning of the
lattice and working downstream, particles are tracked starting from
the exit of each selected element. The betatron coordinates are
initially zero (or very small), while the momentum deviation is
gradually increased until loss of the particle is observed. This
defines the momentum aperture at that location.
In elegant, the algorithm is as follows. For simplicity in
wording, we'll assume the momentum deviations are positive values,
although the method is applied separately for negative values as well:
- Choose a large momentum deviation
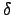 (e.g., 10%) that is sure to be lost, and track.
(e.g., 10%) that is sure to be lost, and track.
- Decrease
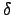 in fairly large steps
in fairly large steps
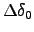 (e.g., 1%) until the particle survives.
Call this momentum deviation
(e.g., 1%) until the particle survives.
Call this momentum deviation 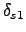 and the previous value (where the particle was lost)
and the previous value (where the particle was lost)
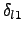 .
.
- Scan outward from
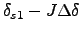 , where the integer
, where the integer 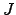 is the ``overstep'' amount,
typically 1.
Use a step-size of
is the ``overstep'' amount,
typically 1.
Use a step-size of
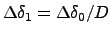 , where
, where 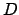 is an integer (typically 10),
not exceeding
is an integer (typically 10),
not exceeding 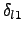 . Stop when a loss occurs. Call this momentum deviation
. Stop when a loss occurs. Call this momentum deviation
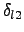 and the last surviving value
and the last surviving value 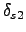 .
.
- If accuracy is acceptable, stop at this point. The momentum aperture is
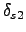 .
.
- If greater accuracy is desired, ``step back'' to a momentum deviation
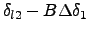 , where
, where 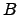 is an integer and scan outward again
with step size
is an integer and scan outward again
with step size
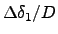 . This procedure is called a ``step-back/split'' and can be
repeated if greater accuracy is desired.
. This procedure is called a ``step-back/split'' and can be
repeated if greater accuracy is desired.


Next: optimize
Up: Namelist Command Dictionary
Previous: matrix_output
Robert Soliday
2006-05-05