


Next: SCRAPER
Up: Element Dictionary
Previous: SCATTER
Tracks through a zero length multipole to simulate space charge effects
Parallel capable? : yes
| Parameter Name |
Units |
Type |
Default |
Description |
This element simulates transverse space charge (SC) kick using
K.Y. Ng's formula ( K.Y. Ng, FNAL, private communication).
The linear SC force is given by:
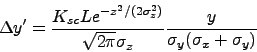 |
(30) |
where
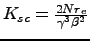 ,
,
 is the integrating length,
is the integrating length,
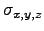 are rms beam size.
are rms beam size.
The non-linear SC force is given by:
![\begin{displaymath}
\Delta y'=\frac{K_{sc}Le^{-z^2/(2\sigma_z^2)}}{2\sigma_z\sqr...
...x}{\sigma_y}}
{\sqrt{2(\sigma_x^2-\sigma_y^2)}}\right)\right ]
\end{displaymath}](img255.gif) |
(31) |
where 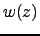 is the complex error function
is the complex error function
![\begin{displaymath}
w(z)=e^{-z^2}\left [ 1+\frac{2i}{\sqrt{\pi}}\int\limits_0^z e^{\zeta^2}d\zeta\right ]
\end{displaymath}](img257.gif) |
(32) |
Equation 31 appear to diverge when
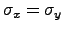 . In fact, this is not
true, because the expressions inside the square brackets will provide zero too at
. In fact, this is not
true, because the expressions inside the square brackets will provide zero too at
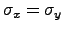 to cancel the poles outside. In our code, we calculate this equation
at
to cancel the poles outside. In our code, we calculate this equation
at 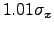 and
and 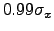 , and average the total effects.
, and average the total effects.
To invoke the calculation, one must use set up command
``insert_sceffects'' proceed ``run_setup'' and ``Twiss_output''
command proceed ``track''.



Next: SCRAPER
Up: Element Dictionary
Previous: SCATTER
Michael Borland
2007-09-07
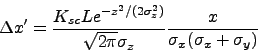
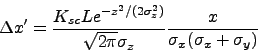
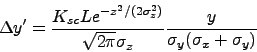
![\begin{displaymath}
\Delta x'=\frac{K_{sc}Le^{-z^2/(2\sigma_z^2)}}{2\sigma_z\sqr...
...x}{\sigma_y}}
{\sqrt{2(\sigma_x^2-\sigma_y^2)}}\right)\right ]
\end{displaymath}](img254.gif)
![\begin{displaymath}
w(z)=e^{-z^2}\left [ 1+\frac{2i}{\sqrt{\pi}}\int\limits_0^z e^{\zeta^2}d\zeta\right ]
\end{displaymath}](img257.gif)