ALPH—An alpha magnet implemented as a matrix, up to 3rd order.

10.1 ALPH—An alpha magnet implemented as a matrix, up to 3rd order.

An alpha magnet implemented as a matrix, up to 3rd order.
Parallel capable? : yes
GPU capable? : yes
Back-tracking capable? : no


Parameter Name	Units	Type	Default	Description

XMAX	M	double	0.0	size of alpha

XS1	M	double	0.0	inner scraper position relative to XMAX

XS2	M	double	0.0	outer scraper position relative to XMAX

DP1		double	-1	inner scraper fractional momentum deviation

DP2		double	1	outer scraper fractional momentum deviation

XPUCK	M	double	-1	position of scraper puck

WIDTHPUCK	M	double	0.0	size of scraper puck

DX	M	double	0.0	misalignment

DY	M	double	0.0	misalignment

DZ	M	double	0.0	misalignment

TILT		double	0.0	rotation about incoming longitudinal axis

PART		short	0	0=full, 1=first half, 2=second half

ORDER		short	0	matrix order [1,3]

GROUP		string	NULL	Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup

This element provides a matrix-based implementation of an alpha magnet [5]. Matrices up to third order are available [4].

The parameter XMAX determines the size of the alpha, which is related to the gradient g in the magnet and the central momentum βγ by

∘ -------- xmax[m ] = 0.07504986 --βγ---. g[T∕m ]

(26)

The path length of the central particle is 2.554x_max .

Because an alpha magnet has large dispersion at the midplane, it is often used for momentum filtration in addition to bunch compression. The dispersion at the center is given by the simple relation

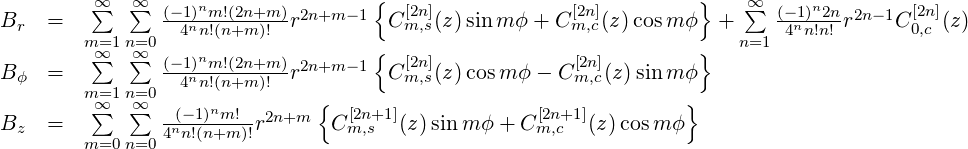R16 = - 1-xmax. 2

(27)

To use an alpha magnet for momentum filtration in elegant, one must split the alpha magnet into two pieces. One may then either use the scraper features of the ALPH element or other elements such as SCRAPER or RCOL.

To split an alpha magnet, one uses the PART parameter. E.g.,

! First half, with momentum filter between -5% and +2.5%
AL1: ALPH,XMAX=0.11,PART=1,DP1=-0.05,DP2=0.025
! Second half
AL2: ALPH,XMAX=0.11,PART=2
AL: LINE=(AL1,AL2)

One can also separate the momentum filtration for better visualization

! First half, with momentum filter between -5% and +2.5%
AL1: ALPH,XMAX=0.11,PART=1
! Momentum filtration
ALM: ALPH,XMAX=0.11,PART=3,DP1=-0.05,DP2=0.025
! Second half
AL2: ALPH,XMAX=0.11,PART=2
! Phase space monitors
WP: WATCH,FILENAME="%s-%ld.wp",MODE="coordinates"
AL: LINE=(WP,AL1,WP,ALM,WP,AL2,WP)

As just illustrated, the parameters DP1 and DP2 may be used to filter the momentum by providing fractional momentum deviation limits. These are implemented in a physical fashion by computing the corresopnding horizontal position deviations and imposing these as limits on the particle coordinates. One may also do this directly using the XS1 and XS2 parameters, which specify maximum acceptable deviations from the nominal horizontal position. XS1 is the allowed deviation on the low-energy side while XS2 is the allowed deviation on the high-energy side.

APCONTOUR

[next] [front] [up]