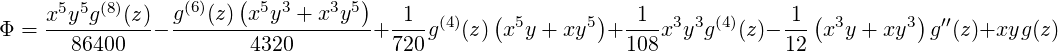 | (31) |
when (x∕a)2 + (y∕b)2 ≤ 1 and 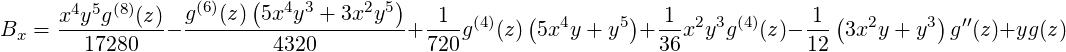 ≤ L∕2, and zero otherwise. The parameters XSIZE and YSIZE are
interpreted as a and b, respectively. L is the length of the slug of charge, which is assumed to be
sufficiently short that the impulse approximation is valid. The computations are based on Furman’s
expressions [60].
≤ L∕2, and zero otherwise. The parameters XSIZE and YSIZE are
interpreted as a and b, respectively. L is the length of the slug of charge, which is assumed to be
sufficiently short that the impulse approximation is valid. The computations are based on Furman’s
expressions [60].
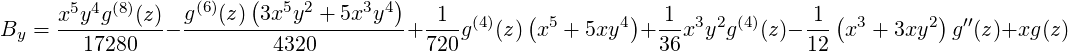 | (32) |
when (x∕a)2 + (y∕b)2 ≤ 1 and 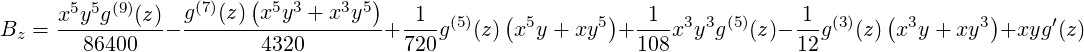 ≤ L∕2, and zero otherwise. The parameters XSIZE and YSIZE are
interpreted as a and b, respectively. L is the length of the slug of charge, which is assumed to be
sufficiently short that the impulse approximation is valid. The computations are based on Furman’s
expressions [60].
≤ L∕2, and zero otherwise. The parameters XSIZE and YSIZE are
interpreted as a and b, respectively. L is the length of the slug of charge, which is assumed to be
sufficiently short that the impulse approximation is valid. The computations are based on Furman’s
expressions [60].