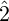
A straight magnetic field element using off-axis expansion from an on-axis derivative.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no
| Parameter Name | Units | Type | Default | Description |
| L | M | double | 0.0 | insertion length |
| LFIELD | M | double | -1 | expected length of the field map for verification purposes only. |
| FILENAME | NULL | STRING | NULL | name of file containing derivative data |
| Z_COLUMN | NULL | STRING | z | name of longitunidal coordinate column in the data file |
| FIELD_COLUMN | NULL | STRING | NULL | name of derivative column in the data file |
| ORDER | short | 1 | order of transverse derivative | |
| EXPANSION_ORDER | short | 0 | order of expansion in x and y. If zero, determined by data in file. |
|
| STRENGTH | NULL | double | 1 | factor by which to multiply field |
| TILT | RAD | double | 0.0 | rotation about longitudinal axis |
| DX | M | double | 0.0 | misalignment |
| DY | M | double | 0.0 | misalignment |
| DZ | M | double | 0.0 | misalignment |
| BX | T | double | 0.0 | add BX*STRENGTH to Bx field |
| BY | T | double | 0.0 | add BY*STRENGTH to By field |
| Z_INTERVAL | short | 1 | input z data is sampled at this interval |
|
| Z_SUBDIVISIONS | short | 1 | Number of subdivisions of z interval to use in integration |
|
| SYNCH_RAD | short | 0 | if nonzero, include classical, single-particle synchrotron radiation |
|
| ISR | short | 0 | if nonzero, include incoherent synchrotron radiation (quantum excitation) |
|
| PARTICLE_OUTPUT_FILE | STRING | NULL | name of file for phase-space and field output. Use for debugging only in serial version. |
|
BOFFAXE continued
A straight magnetic field element using off-axis expansion from an on-axis derivative.
| Parameter Name | Units | Type | Default | Description |
| FIELD_OUTPUT_FILE | NULL | STRING | NULL | name of file to which a grid of field values will be written. Disabled for parallel version. |
| NX_OUTPUT | NULL | long | 0 | Number of x sample points for field output |
| NY_OUTPUT | NULL | long | 0 | Number of y sample points for field output |
| X_HALF_SPAN_OUTPUT | NULL | double | -1 | Half-span of x sample points for field output |
| Y_HALF_SPAN_OUTPUT | NULL | double | -1 | Half-span of y sample points for field output |
| GROUP | string | NULL | Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup |
|
This experimental element simulates transport through a 3D magnetic field constructed from an off-axis expansion. At present, it is restricted to non-bending elements and in fact to quadrupoles and sextupoles.
This method of expanding the fields is prone to corruption by noise, to a much greater degree than the generalized gradient expansion used by BGGEXP. However, it uses data that can very readily be obtained from magnetic measurements with a Hall probe. Users are cautioned to take care in deciding how far to trust the expansion.
For quadrupoles, we use the on-axis gradient g(z) and its z derivatives g(n)(z) The scalar potential can be written
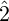 | (35) |
From which we find
 | (36) |
 | (37) |
and
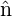 | (38) |
These equations satisfy Maxwell’s curl equation exactly while satisfying the divergence equation to 10th order. A similar expansion is available in the code for sextupoles.
For quadrupoles, at minimum the z-dependent gradient B1(z) must be given, while for sextupoles B2(z) is required. Bn(z) is specified in the column named by the FIELD_COLUMN parameter. The names for the columns containing z derivatives of Bn(z) are constructed from the name of the primary column. Assume for concreteness that FIELD_COLUMN="Gradient". elegant looks for Bn(1)(z) in column GradientDeriv and Bn(m)(z) for m > 1 in columns GradientDeriv2, GradientDeriv3, etc. Even if the expansion is limited by the ORDER parameter, all gradients will be used for interpolation with respect to z if the Z_SUBDIVISIONS parameter is larger than 1. The expansion is truncated if the needed columns do not exist in the input file.
The needed derivatives can be obtained using the program sddsderiv, e.g.,
(In this example, we use a Savitzky-Golay filter to compute the first three z derivatives of g(z) using a 7th order fit with 7 points ahead of and behind the evaluation location.) The file gradients.sdds would then be given as the value of FILENAME.
High-order numerical derivative are of course prone to corruption by measurement noise. Examining the derivatives is strongly recommended to ensure this is not an issue.
BRANCH