10.11 BUMPER—A time-dependent kicker magnet with optional spatial dependence of
the kick and no fringe effects. The waveform is in SDDS format, with time in seconds and
amplitude normalized to 1. The optional spatial dependence is also specified as an SDDS
file.
A time-dependent kicker magnet with optional spatial dependence of the kick and no fringe effects. The
waveform is in SDDS format, with time in seconds and amplitude normalized to 1. The optional spatial
dependence is also specified as an SDDS file.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| L | M | double | 0.0 | length |
|
|
|
|
|
| ANGLE | RAD | double | 0.0 | kick angle |
|
|
|
|
|
| TILT | RAD | double | 0.0 | rotation about longitudinal
axis |
|
|
|
|
|
| DX | M | double | 0.0 | misalignment |
|
|
|
|
|
| DY | M | double | 0.0 | misalignment |
|
|
|
|
|
| DZ | M | double | 0.0 | misalignment |
|
|
|
|
|
| B2 | 1∕M2 | double | 0.0 | Sextupole term:
By=Bo*(1+b2*x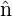 ) ) |
|
|
|
|
|
| TIME_OFFSET | S | double | 0.0 | time offset of waveform |
|
|
|
|
|
| PERIODIC | | long | 0 | is waveform periodic? |
|
|
|
|
|
| PHASE_REFERENCE | | long | 0 | phase reference
number (to link with other
time-dependent elements) |
|
|
|
|
|
| FIRE_ON_PASS | | long | 0 | pass number to fire on |
|
|
|
|
|
| N_KICKS | | long | 0 | Number of kicks to use for
simulation. 0 uses an exact
result but ignores b2. |
|
|
|
|
|
| WAVEFORM | | STRING | NULL | <filename>=<x>+<y>
form specification of input file
giving kick factor vs time |
|
|
|
|
|
| DEFLECTION_MAP | | STRING | NULL | optional filename
giving the spatial variation of
the deflection |
|
|
|
|
|
| GROUP | | string | NULL | Optionally used to assign an
element to a group, with
a user-defined name. Group
names will appear in the
parameter output file in the
column ElementGroup |
|
|
|
|
|
| |
This element simulates a time-dependent kicker magnet as a rectangular dipole with no fringe
field effects. To use this element, you must supply an SDDS file giving the time-dependent
waveform. The element is called BUMPER to because HKICK, VKICK, KICKER are used for steering
magnets.
The arrival time of the beam is taken to define the reference time, t = 0. Hence, if the waveform file
has the maximum amplitude at t = 0, the beam will get kicked at the peak of the waveform. If the
waveform peaks at t = tpeak, then setting TIME_OFFSET equal to -tpeak will ensure that the beam is kicked
at the peak amplitude.
By default, the kicker fires on the first beam passage. However, if FIRE_ON_PASS is used, then the
kicker is treated like a drift space until the specified pass. Note that the first pass is 0, not
1.
If PHASE_REFERENCE is non-zero, then the initial timing is taken from the first time-dependent element
that has the same PHASE_REFERENCE value. This would allow, for example, simulating several kickers firing
at the same time. Delays relative to this reference time can then be given with positive adjustments to
TIME_OFFSET.
The waveform input file need not have equispaced points in time. However, the time values should
increase monotonically.
The deflection map, if provided, should have four floating-point columns
- Transverse coordinates x and y, with units of m.
- Kick multipliers xpFactor and ypFactor, which are dimensionless quantities.
The resulting kick in each plane for a particle with coordinates (x,y,t,δ) is
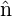 | (39) |
where q stands for x or y, θ is the specfied deflection angle, A(t) is the time-dependent amplitude
waveform, and fq(x,y) is the deflection map factor for the q plane at the particle’s location.
The data in the deflection map file must be sorted so that x changes fastest, which can be
accomplished using the command
sddssort input.sdds -column=y,incr -column=x,incr
This element simulates a dipole kicker only. For multipole kickers, see the MBUMPER element.
Explanation of <filename>=<x>+<y> format: Several elements in elegant make
use of data from external files to provide input waveforms. The external files are SDDS files,
which may have many columns. In order to provide a convenient way to specify both the
filename and the columns to use, we frequently employ <filename>=<x>+<y> format for the
parameter value. For example, if the parameter value is waveform.sdds=t+A, then it means
that columns t and A will be taken from file waveform.sdds. The first column is always the
independent variable (e.g., time, position, or frequency), while the second column is the dependent
quantity.
 )
)