KICKER—A combined horizontal-vertical steering magnet implemented as a matrix, up to 2nd order. For time-dependent kickers, see BUMPER.

A combined horizontal-vertical steering magnet implemented as a matrix, up to 2nd order. For time-dependent kickers, see BUMPER.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no


Parameter Name	Units	Type	Default	Description

L	M	double	0.0	length

HKICK	RAD	double	0.0	x kick angle

VKICK	RAD	double	0.0	y kick angle

TILT	RAD	double	0.0	rotation about longitudinal axis

B2	1∕M²	double	0.0	normalized sextupole strength (e.g., kick = KICK(1+B2x))

HCALIBRATION		double	1	factor applied to obtain x kick

VCALIBRATION		double	1	factor applied to obtain y kick

EDGE_EFFECTS		long	0	include edge effects?

ORDER		long	0	matrix order

STEERING		long	1	use for steering?

SYNCH_RAD		long	0	include classical, single-particle synchrotron radiation?

ISR		long	0	include incoherent synchrotron radiation (quantum excitation)?

LERAD		double	0.0	if L=0, use this length for radiation computations

GROUP		string	NULL	Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup

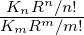10.49 KICKER—A combined horizontal-vertical steering magnet implemented as a matrix, up to 2nd order. For time-dependent kickers, see BUMPER.