10.64 MARK—A marker, equivalent to a zero-length drift space.
A marker, equivalent to a zero-length drift space.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : yes
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| DX | M | double | 0.0 | non-functional misalignment
(e.g., for girder) |
|
|
|
|
|
| DY | M | double | 0.0 | non-functional misalignment
(e.g., for girder) |
|
|
|
|
|
| FITPOINT | | short | 0 | Supply local values of Twiss
parameters, moments, floor
coordinates, matrices, etc. for
optimization? |
|
|
|
|
|
| GROUP | | string | NULL | Optionally used to assign an
element to a group, with
a user-defined name. Group
names will appear in the
parameter output file in the
column ElementGroup |
|
|
|
|
|
| |
If FITPOINT=0, this element results only in generation of additional output rows in the various files
that contain output vs s. For example, Twiss parameters, closed orbits, and matrices vs s will all contain a
row for each occurrence of each marker element.
If FITPOINT=1, the element has additional functionality in the context of optimizations. In particular,
for occurrence N of the defined element Element, a series of symbols are created of the form
Element#N.quantity, where quantity has the following values:
- The quantity pCentral will be available, giving the reference value of βγ at the marker
location.
- The quantities Cx, Cxp, Cy, Cyp, Cs, and Cdelta will be available, giving coordinate centroid
values from tracking to the marker location.
- The quantities Sx, Sxp, Sy, Syp, Ss, and Sdelta will be available, giving coordinate rms values
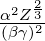 at the marker location from tracking.
at the marker location from tracking.
- The quantity Particles will be available, giving the number of particles tracked to the marker
location.
- The quantities sij will be available, giving ⟨(xi-⟨xi⟩)(xj-⟨xj⟩)⟩ from tracking at the marker
location, where 1 ≤ i ≤ 6 and i < j ≤ 6.
- The quantities betaxBeam, alphaxBeam, betayBeam, and alphayBeam, which are the twiss
parameters computed from the beam moments obtained by tracking, will be available.
- The quantities Rij will be available, for 1 ≤ i ≤ 6 and 1 ≤ j ≤ 6, giving the accumulated
first-order transport matrix to the marker location.
- If the default matrix order (as set in run_setup) is 2 or greater, the quantities Tijk will be
available, for 1 ≤ i ≤ 6, 1 ≤ j ≤ 6, and 1 ≤ k ≤ j, giving the accumulated second-order
transport matrix to the marker location.
- If Twiss parameter calculations are being performed
(via twiss_output with output_at_each_step=1), then the quantities alphax, betax, nux,
psix, etax, etapx, and etaxp, along with similarly-named quantities for the vertical plane,
will be available, giving twiss parameter values at the marker location. Note that etapx and
etaxp are the same, being alternate names for ηx′. If radiation integrals are requested, the
values of the radiation integrals are available in the quantities I1, I2, etc.
- If coupled Twiss parameter calculations are being performed (via coupled_twiss_output
with output_at_each_step=1), then the quantities betax1, betax2, betay1, betay2, cetax,
cetay, and tilt will be available. (These are the two beta functions for x and y, the coupled
dispersion values for x and y, and the beam tilt).
- If moments calculations are
being performed (via moments_output with output_at_each_step=1), then the quantities
sijm, 1 ≤ i ≤ j ≤ 6, giving the 21 unique elements of the sigma matrix, are available, as
are sijbetam, 1 ≤ i ≤ j4, giving the 6 unique elements with the dispersive terms removed.
The quantities cim, 1 ≤ i ≤ 6, are also created, giving the 6 centroids from the moments
computation. The projected betatron emittances are available using exbeta and eybeta. In
addition, the emittances of the three modes are available using eim, 1 ≤ i ≤ 3, without any
prefix. The m on the end of the symbols is to distinguish them from the moments computed
from tracking.
- If floor coordinate calculations are begin performed (via floor_coordinates), then the
quantities X, Y, Z, theta, phi, psi, and s will be available. These are, respectively, the three
position coordinates, the three angle coordinates, and the total arc length at the marker
location.
The misalignment controls for this element are non-functional, in the sense that they do not affect the
beam. However, when combined with external scripts and the GROUP parameter, one can use this feature
to implement girder misalignments using pairs of markers to indicate the ends of the girders. A future
version of elegant will implement this internally.
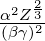 at the marker location from tracking.
at the marker location from tracking.
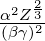 at the marker location from tracking.
at the marker location from tracking.