7.73 twiss_output
- type: action/setup command.
- function: compute and output uncoupled Twiss parameters, or set up to do so.
- sequence: must follow run_setup.
- Command syntax, including use of equations and subcommands, is discussed in 7.2.
- N.B.: the output of this command is strictly correct only when the beamline has vanishingly
small x-y coupling. For rings, use of coupled_twiss_output is an option when that
requirement is not sufficiently well satisfied.
&twiss_output
STRING filename = NULL;
long matched = 1;
long output_at_each_step = 0;
long output_before_tune_correction = 0;
long final_values_only = 0;
long statistics = 0;
long radiation_integrals = 0;
long concat_order = 3;
long higher_order_chromaticity = 0;
long higher_order_chromaticity_points = 5;
double higher_order_chromaticity_range = 4e-4;
double chromatic_tune_spread_half_range = 0;
long quick_higher_order_chromaticity = 0;
double beta_x = 1;
double alpha_x = 0;
double eta_x = 0;
double etap_x = 0;
double beta_y = 1;
double alpha_y = 0;
double eta_y = 0;
double etap_y = 0;
STRING reference_file = NULL;
STRING reference_element = NULL;
long reference_element_occurrence = 0;
long reflect_reference_values = 0;
long cavities_are_drifts_if_matched = 1;
long compute_driving_terms = 0;
long leading_order_driving_terms_only = 0;
STRING s_dependent_driving_terms_file = NULL;
long local_dispersion = 1;
&end
The output file from this command contains the following columns, giving values of quantities at the
exit of each element, unless otherwise noted.
- s — The arc length.
- ElementName — The name of the element.
- ElementType — The type name of the element.
- betax and betay — The horizontal and vertical beta functions.
- alphax and alphay — The horizontal and vertical alpha functions, where α = -
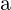 .
.
- psix and psiy — The horizontal and vertical betatron phase advance in radians.
- etax and etay — The horizontal and vertical dispersion functions.
- etaxp and etayp — The slopes of the horizontal and vertical dispersion functions.
- xAperture and yAperture — The horizontal and vertical apertures. If undefined, will have a
value of 10m. If the beam trajectory is non-zero, then the aperture will be changed (usually
reduced) accordingly. Hence, these are best understood as the effective apertures. They
are used in determining the horizontal and vertical acceptance parameters, Ax and Ay.
- pCentral0 — The central momentum (βγ) at the entrance to the element.
- dIn — Contribution to radiation integral In. Radiation integrals take account of horizontal
bending only.
The output file contains the following parameters. Note that chromatic quantities depend on the order
settings of the individual elements, the default order (in run_setup), and the concatenation order given in
the twiss_output command. These quantities pertain to the end of the lattice or to the lattice as a
whole.
- nux and nuy — The horizontal and vertical tunes.
- dnux/dp and dnuy/dp — The horizontal and vertical chromaticities, defined as dν∕dδ.
- dnux/dp2 and dnuy/dp2 — The horizontal and vertical 2nd-order chromaticities, defined as
d2ν∕dδ2. Will be zero if higher_order_chromaticity is zero.
- dnux/dp3 and dnuy/dp3 — The horizontal and vertical 3rd-order chromaticities, defined as
d3ν∕dδ3. Will be zero if higher_order_chromaticity is zero.
- dbetax/dp and dbetay/dp — Chromatic derivatives of the horizontal and vertical beta
functions, defined as
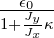 .
.
- dalphax/dp and dalphay/dp — Chromatic derivatives of the horizontal and vertical alpha
functions, defined as
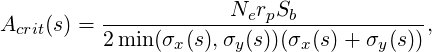 .
.
- etax2, etax3, etay2, etay3 — Higher order dispersion in the horizontal and vertical planes.
For example, for the horizontal plane, the closed orbit at the end of the lattice depends on δ
according to x = ηxδ + ηx2δ2 + ηx3δ3. This differs from the chromaticity expansion, which is
given in terms of successive derivatives of ν(δ).
- dnux/dAx, dnux/dAy, dnuy/dAx, dnuy/dAy — Tune shifts with amplitude, where amplitude
is defined as Aq = (1 + αq)q2∕βq, with q = x or q = y. These will be zero unless the
tune_shift_with_amplitude command is given.
- h11001, h00111, h20001, h00201, h10002, h21000, h30000, h10110, h10020, h10200, h22000,
h11110, h00220, h31000, h40000, h20110, h11200, h20020, h20200, h00310, h00400—
Resonance driving terms[29]. These will be zero unless compute_driving_terms is nonzero.
See table 2 for an explanation of each term.
- dnux/dJx, dnux/dJy, and dnuy/dJy — Tune shifts with amplitude from Bengtsson’s
theory [29]. Note that Jq =
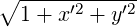 , where q is x or y. See documentation for
tune_shift_with_amplitude for discussion and comparison with dnux/dAx etc. These will
be zero unless compute_driving_terms is nonzero.
, where q is x or y. See documentation for
tune_shift_with_amplitude for discussion and comparison with dnux/dAx etc. These will
be zero unless compute_driving_terms is nonzero.
- Ax and Ay — The horizontal and vertical acceptance. These will be zero if no apertures are
defined.
- alphac, alphac2, alphac3 — First-, second, and third-order momentum compaction. The
path length is s = so + αcLδ + αc2Lδ2 + αc3Lδ2. Regarding αc3, users are cautioned that the
analytical matrices for most elements are limited to second-order, so using tracking-derivce
matrices is necessary where supported, and gives limited accuracy.
- couplingIntegral, couplingDelta, and emittanceRatio — These quantities are defined
in section 3.1.4.4 of [19]. The computations include tilted quadrupoles, vertical orbit in
sextupoles, vertical sextupole displacement, and solenoids. Note that the emittance ratio does
not include the effect of vertical dispersion.
- In — The nth radiation integral.
- taux, tauy, taudelta — Radiation damping times for x, y, and δ.
- Jx, Jy, Jdelta — Damping partition factors for x, y, and δ.
- ex0, enx0 — Horizontal equilibrium geometric and normalized emittances.
- Sdelta0 — Equilibrium fractional rms energy spread.
- U0 — Energy loss per turn.
N.B.: the higher-order dispersion and higher-order chromaticity are computed using the concatenated
third-order matrix. However, elegant only has third-order matrices for three elements: alpha magnets,
quadrupoles, and sextupoles. This may be acceptable if any dipoles (for example) have large bending
radius. Users who are concerned about these effects should perform off-energy tracking using canonical
elements (i.e., CSBEND, KQUAD, KSEXT, and MULT), which include energy dependence to all
orders.
Also, note that by default all elements are computed to second order only. You must change the
default\_order parameter on run\_setup to 3 in order to use the third-order matrices for alpha
magnets, quadrupoles, and sextupoles. You may also use the ORDER parameter on individual element
definitions.
Table 2: Meaning of the various driving terms[29].
|
|
| Term Name | Explanation |
|
|
|
|
| h11001 | drives x chromaticity |
|
|
| h00111 | drives y chromaticity |
|
|
| h20001 | drives synchro-betatron resonances |
|
|
| h00201 | drives momentum-dependence of beta functions |
|
|
| h10002 | drives second order dispersion |
|
|
| h21000 | drives νx |
|
|
| h30000 | drives 3νx |
|
|
| h10110 | drives νx |
|
|
| h10020 | drives νx - 2νy |
|
|
| h10200 | drives νx + 2νy |
|
|
| h22000 | drives dνx∕dJx |
|
|
| h11110 | drives dνx∕dJy |
|
|
| h00220 | drives dνy∕dJy |
|
|
| h31000 | drives 2νx |
|
|
| h40000 | drives 4νx |
|
|
| h20110 | drives 2νx |
|
|
| h11200 | drives 2νy |
|
|
| h20020 | drives 2νx - 2νy |
|
|
| h20200 | drives 2νx + 2νy |
|
|
| h00310 | drives 2νy |
|
|
| h00400 | drives 4νy |
|
|
| |
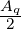 , where δ was the local
fractional momentum deviation. In a linear system, the local dispersion is related to the beam
moments by ηx = ⟨xδ⟩∕⟨δ2⟩. In a linac or other systems with rf elements, one might also be
interested in the “global” dispersion
, where δ was the local
fractional momentum deviation. In a linear system, the local dispersion is related to the beam
moments by ηx = ⟨xδ⟩∕⟨δ2⟩. In a linac or other systems with rf elements, one might also be
interested in the “global” dispersion 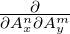 , where δ0 is the energy deviation at the beginning
of the system. In this case, set local_dispersion=0. Alternatively, one may look at the Ri6
elements of the matrix from matrix_output.
, where δ0 is the energy deviation at the beginning
of the system. In this case, set local_dispersion=0. Alternatively, one may look at the Ri6
elements of the matrix from matrix_output.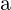 .
.
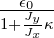 .
.
 .
.
 , where
, where