

Next: RFTMEZ0
Up: Element Dictionary
Previous: RFMODE
Tracks through a TM110-mode (deflecting) rf cavity with all magnetic and electric field components. NOT RECOMMENDED--See below.
Parallel capable? : yes
| Parameter Name |
Units |
Type |
Default |
Description |
| PHASE |
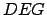 |
double |
0.0 |
phase |
| TILT |
 |
double |
0.0 |
rotation about longitudinal axis |
| FREQUENCY |
 |
double |
2856000000 |
frequency |
| VOLTAGE |
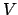 |
double |
0.0 |
peak deflecting voltage |
| PHASE_REFERENCE |
|
long |
0 |
phase reference number (to link with other time-dependent elements) |
| VOLTAGE_WAVEFORM |
|
STRING |
NULL |
 filename filename = = x x + + y y form specification of input file giving voltage waveform factor vs time form specification of input file giving voltage waveform factor vs time |
| VOLTAGE_PERIODIC |
|
long |
0 |
If non-zero, voltage waveform is periodic with period given by time span. |
| ALIGN_WAVEFORMS |
|
long |
0 |
If non-zero, waveforms' t=0 is aligned with first bunch arrival time. |
| VOLTAGE_NOISE |
|
double |
0.0 |
Rms fractional noise level for voltage. |
| PHASE_NOISE |
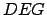 |
double |
0.0 |
Rms noise level for phase. |
| GROUP_VOLTAGE_NOISE |
|
double |
0.0 |
Rms fractional noise level for voltage linked to group. |
| GROUP_PHASE_NOISE |
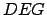 |
double |
0.0 |
Rms noise level for phase linked to group. |
| VOLTAGE_NOISE_GROUP |
|
long |
0 |
Group number for voltage noise. |
| PHASE_NOISE_GROUP |
|
long |
0 |
Group number for phase noise. |
NB: Although this element is correct insofar as it uses the
fields for a pure TM110 mode, it is recommended that the RFDF
element be used instead. In a real deflecting cavity with entrance
and exit tubes, the deflecting mode is a hybrid TE/TM mode, in which
the deflection has no dependence on the radial coordinate.
To derive the field expansion, we start with some results from
Jackson[16], section 8.7. The longitudinal electric field
for a TM mode is just
 |
(14) |
where  is an integer,
is an integer,  is the length of the cavity, and we use
cylindrical coordinates
is the length of the cavity, and we use
cylindrical coordinates
 . The factor of
. The factor of  represents a
choice of sign and phase convention. We are interested in the
TM110 mode, so we set
represents a
choice of sign and phase convention. We are interested in the
TM110 mode, so we set  . In this case, we have
. In this case, we have
 |
(15) |
and (using CGS units)
 |
(16) |
For a cylindrical cavity, the function  for the
for the  aximuthal mode is
aximuthal mode is
 |
(17) |
where  ,
,  is the first zero of
is the first zero of  , and
, and  is the cavity radius.
We don't need to know the cavity radius, since
is the cavity radius.
We don't need to know the cavity radius, since  , where
, where  is the
resonant frequency. By choosing
is the
resonant frequency. By choosing  for the aximuthal dependence, we'll get
a magnetic field primarily in the vertical direction.
for the aximuthal dependence, we'll get
a magnetic field primarily in the vertical direction.
In MKS units, the magnetic field is
 |
(18) |
Using mathematica, we expanded these expressions to sixth order
in  . Here, we present only the expressions to second
order. Taking the real parts only, we now have
. Here, we present only the expressions to second
order. Taking the real parts only, we now have
The Cartesian components of  can be computed easily
can be computed easily
The Lorentz force on an electron is
 ,
giving
,
giving
We see that for
 , we have
, we have  ,
,  , and
, and
 |
(29) |
Hence, for  and
and  we have
we have  . This explains
our choice of sign and phase convention above. Indeed, owing to the
factor of
. This explains
our choice of sign and phase convention above. Indeed, owing to the
factor of  , we have a peak deflection of
, we have a peak deflection of  , where
, where  is
the cavity length and
is
the cavity length and  the beam energy. Thus, if
the beam energy. Thus, if  is
specified in volts, and the beam energy expressed in electron volts,
the deflection is simply the ratio of the two. As a result, we've
chosen to parametrize the deflection strength simply by referring to
the ``deflecting voltage,''
is
specified in volts, and the beam energy expressed in electron volts,
the deflection is simply the ratio of the two. As a result, we've
chosen to parametrize the deflection strength simply by referring to
the ``deflecting voltage,'' 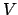 .
.


Next: RFTMEZ0
Up: Element Dictionary
Previous: RFMODE
Robert Soliday
2007-04-02
![]() . Here, we present only the expressions to second
order. Taking the real parts only, we now have
. Here, we present only the expressions to second
order. Taking the real parts only, we now have




![]() ,
giving
,
giving