8.18 sddsmatchtwiss

• description: sddsmatchtwiss transforms a beam of macro-particles to match to given beta functions and dispersion. This can be useful in taking macro-particle data from one simulation and using it in another. For example, a beam file from PARMELA could be given the right beta functions for use with a specific lattice in an elegant run, saving the trouble of rematching to join the two simulations. Similarly, a beam from elegant could be matched into an FEL simulation.
• examples:

  sddsmatchtwiss elegantBeam.out FELBeam.in -xPlane=beta=1.0,alpha=-0.2 -yPlane=beta=0.5,alpha=0.2

• synopsis:

  sddsmatchtwiss [-pipe=[input][,output]] inputfile outputfile [-saveMatrices=filename] [-loadMatrices=filename] [-xPlane=[beta=meters,alpha=value][,etaValue=meters][,etaSlope=value]] [-yPlane=[beta=meters,alpha=value][,etaValue=meters][,etaSlope=value]] [-zPlane=[deltaStDev=value][,tStDev=value] [,correlation=seconds|alpha=value][,chirp=1/seconds][,betaGamma=value]] [-nowarnings]

• files:

  inputfile is an SDDS file containing one or more pages of data giving the phase-space coordinates of macro particles. The macro particle data is stored in columns named x, xp, y, yp, and p. The units are those used by elegant for the output file from run_setup, the bunch file from bunched_beam, and the coordinate-mode output from the WATCH element. The data from these columns is used together with the commandline arguments to produce new values for these columns; the new values are delivered to outputfile. Other columns may be present in inputfile; if so, they are passed to outputfile unchanged.

• switches:
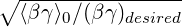
  • -xPlane=[beta=meters,alpha=value][,etaValue=meters][,etaSlope=value] — Specifies the desired parameters for the beam in the horizontal plane. beta and alpha give β and α = -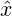; they must both be given or both be omitted. etaValue and etaSlope give the dispersion, η, and its slope, .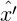
  • -yPlane=[beta=meters,alpha=value][,etaValue=meters][,etaSlope=value] — Same as -xPlane, except for the vertical plane.
  • -zPlane=[deltaStDev=value][,tStDev=value] [,{correlation=seconds|alpha=value}][,chirp=seconds][,betaGamma=value] — deltaStDev is σ_δ = ⟨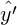, tStDev is σ_t = ⟨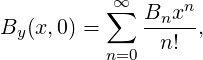, and correlation is σ_t,δ = ⟨(δ -⟨δ⟩)((t -⟨t⟩)⟩, in terms of which the longitudinal emittance is ϵ = 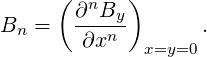. alpha is -σ_t,δ∕ϵ. The chirp, if requested, is added after generation of the beam according to the other parameters. If betaGamma is given, the beam is “accelerated” to the given average value of βγ in a idealized sense, preserving the momentum spread and transforming the transverse coordinates by the factor .
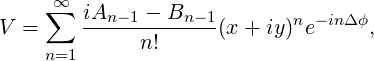  • -saveMatrices=filename — Requests saving the transformation matrices to a file.
  • -loadMatrices=filename — Requests loading the transformation matrices from a file.
  • -nowarnings — Suppresses warning messages.
• authors: M. Borland, H. Shang, ANL/APS.