[tail] [up]

9.1 Magnet Strength

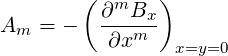
There are many conventions for specifying magnetic fields in terms of a multipole, polynomial, or Taylor expansion, which leads to potential confusion. In elegant (as in MAD[2]), magnet strengths are specified in terms of Taylor series. For normal multipoles and y = 0, the expansion is

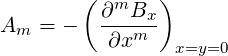∑∞ Bnxn By(x,0) = -----, n=0 n!
(16)

where B0 is the dipole, B1 is the quadrupole, etc. In general,

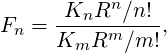( n ) B = ∂-By- . n ∂xn x=y=0
(17)

elegant follows MAD [2] in using a right-handed coordinate system (x,y,z) in which z is along the beam direction, x is to the left, and y is up.

This expansion for the normal multipole terms can be related to a multipole expansion that includes both normal and skew components. In this convention, positive normal multipole coefficients give positive By for x > 0 and y = 0. Rotating a positive normal multipole with N poles π∕N clockwise about the vector along the beam direction will convert it into a positive skew multipole. As a result, for a positive skew multipole, By will be non-negative and Bx will be negative for x > 0 along the line ϕ = π∕N.

We can satisfy these conventions if we write the scalar potential as

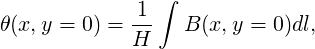∑∞ iAn -1 - Bn-1 V = -------------(x + iy)ne-inΔϕ, n=1 n!
(18)

where, as we’ll see, Am are skew components and Bm are normal components for a 2(m + 1)-pole. The coordinates (x,y) are in a right-handed system with the longitudinal coordinate z. Δϕ is the rotation angle of the magnet, where a clockwise rotation about the nominal trajectory corresponds to Δϕ > 0. The minus sign in e-inΔϕ is because we rotate the magnet while keeping the coordinate system fixed.

The magnetic fields are

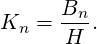∑∞ By = - ℑ ∂V-= ℑ An-+-iBn-(x+ iy)ne-i(n+1 )Δ ϕ, ∂y n=0 n!
(19)

and

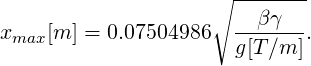∞∑ Bx = - ℑ ∂V- = ℑ --iAn-+-Bn-(x + iy)ne-i(n+1)Δϕ, ∂x n=0 n!
(20)

We can relate the coefficients to the Bm quantities used in MAD and elegant by noting that for Δϕ = 0

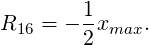(∂mBy ) Bm = ---m-- ∂x x=y=0
(21)

and

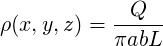( m ) Am = - ∂--Bx- ∂xm x=y=0
(22)

Note the minus sign in the last equation, which differs from commonly asserted conventions.

Multipole errors are typically specified as fractions of the main field harmonic at a reference radius R, e.g.,

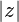K Rn∕n! Fn = --n--m----, KmR ∕m!
(23)

where m is the main harmonic and n is the error harmonic.

For electrons, the deflection from a thin element is

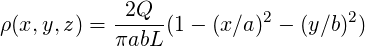∫ θ(x,y = 0) = -1 B (x,y = 0)dl, H
(24)

where H = Bρ = -p∕e is the beam rigidity and p = mecβγ is the momentum. The geometric strengths Kn are defined as

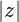Bn- Kn = H .
(25)

By convention in elegant, a positive Kn value deflects a particle at x > 0 toward x = 0. E.g., a positive K1 value indicates a horizontally focusing quadrupole.

[front] [up]