| Parameter Name | Units | Type | Default | Description |
| L | M | double | 0.0 | length |
| KICK | RAD | double | 0.0 | kick strength |
| TILT | RAD | double | 0.0 | rotation about longitudinal axis |
| B2 | 1∕M2 | double | 0.0 | normalized sextupole strength
(kick = KICK*(1+B2*x |
| CALIBRATION | double | 1 | strength multiplier |
|
| EDGE_EFFECTS | short | 0 | include edge effects? |
|
| ORDER | short | 0 | matrix order | |
| STEERING | short | 1 | use for steering? |
|
| SYNCH_RAD | short | 0 | include classical, single-particle synchrotron radiation? |
|
| ISR | short | 0 | include incoherent synchrotron radiation (quantum excitation)? |
|
| LERAD | double | 0.0 | if L=0, use this length for radiation computations |
|
| GROUP | string | NULL | Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup |
|
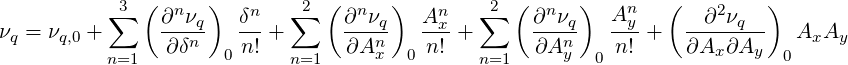 )
when y=0)
)
when y=0)