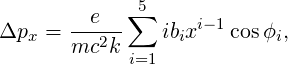
A first-order matrix RF cavity with exact phase dependence, plus optional amplitude and phase
modulation.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no
| Parameter Name | Units | Type | Default | Description |
| L | M | double | 0.0 | length |
| VOLT | V | double | 0.0 | nominal voltage |
| PHASE | DEG | double | 0.0 | nominal phase |
| FREQ | Hz | double | 500000000 | nominal frequency |
| Q | double | 0.0 | cavity Q |
|
| PHASE_REFERENCE | long | 0 | phase reference number (to link with other time-dependent elements) |
|
| AMMAG | double | 0.0 | magnitude of amplitude modulation (fraction value) |
|
| AMPHASE | DEG | double | 0.0 | phase of amplitude modulation |
| AMFREQ | Hz | double | 0.0 | frequency of amplitude modulation |
| AMOFFSET | DEG | double | 0.0 | offset of amplitude modulation |
| AMDECAY | 1∕s | double | 0.0 | exponential decay rate of amplitude modulation |
| PMMAG | DEG | double | 0.0 | magnitude of phase modulation |
| PMPHASE | DEG | double | 0.0 | phase of phase modulation |
| PMFREQ | Hz | double | 0.0 | frequency of phase modulation |
| PMOFFSET | DEG | double | 0.0 | offset of phase modulation |
| PMDECAY | 1∕s | double | 0.0 | exponential decay rate of phase modulation |
| START_TIME | S | double | 0.0 | start time for applying modulation |
| END_TIME | S | double | -1 | end time for applying modulation |
| FIDUCIAL | STRING | NULL | mode for determining fiducial arrival time (light, tmean, first, pmaximum) |
|
| RECORD | STRING | NULL | output file for cavity data |
|
| GROUP | string | NULL | Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup |
|
This element is very similar to the RFCA element, except that the amplitude and phase of the cavity can be modulated.
The phase convention is as follows, assuming a positive rf voltage: PHASE=90 is the crest for acceleration. PHASE=180 is the stable phase for a storage ring above transition without energy losses.
The element works by first computing the fidicial arrival time . Using this, the effective voltage is computed using the amplitude modulation parameters, according to
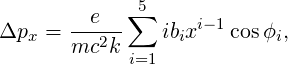 | (96) |
where V 0 is the nominal cavity voltage VOLT, Aam is AMMAG, ωam is the angular frequency corresponding to AMFREQ, ϕam is the amplitude modulation phase corresponding to AMPHASE (converted from degrees to radians), and αam is AMDECAY.
The phase of the phase modulation is computed using
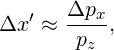 | (97) |
where ωpm is the angular frequency corresponding to PMFREQ and Δϕpm is the phase offset corresponding to PMPHASE (converted from degrees to radians). The rf phase for the centroid is then computed using
 | (98) |
where ω0 is the nominal rf angular frequency (corresponding to FREQ), ϕ0 corresponds to PHASE (converted to radians), Φm corresponds to PMMAG (converted to radians), and αpm corresponds to PMDECAY.
The effective instantaneous rf angular frequency is
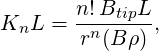 | (99) |
Using all of the above, the voltage seen by a particle arriving at time t is then
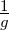 | (100) |
MONI