
A canonical kick multipole.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no
| Parameter Name | Units | Type | Default | Description |
| L | M | double | 0.0 | length |
| KNL | M-ORDER | double | 0.0 | integrated geometric strength |
| TILT | RAD | double | 0.0 | rotation about longitudinal axis |
| BORE | M | double | 0.0 | bore radius |
| BTIPL | TM | double | 0.0 | integrated field at pole tip, used if BORE nonzero |
| DX | M | double | 0.0 | misalignment |
| DY | M | double | 0.0 | misalignment |
| DZ | M | double | 0.0 | misalignment |
| FACTOR | double | 1 | factor by which to multiply strength |
|
| ORDER | short | 1 | multipole order |
|
| SYNCH_RAD | short | 0 | include classical, single-particle synchrotron radiation? |
|
| EXPAND_HAMILTONIAN | short | 0 | If 1, Hamiltonian is expanded to leading order. |
|
| MATRIX_ORDER | short | 0 | matrix order |
|
| N_SLICES | long | 4 | Number of slices (full integrator steps). |
|
| N_KICKS | long | 4 | Deprecated. Use N_SLICES. |
|
| GROUP | string | NULL | Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup |
|
This element simulates a multipole element using 4th-order sympletic integration. A single multipole order, n, is given. The multipole strength is specified by giving
 | (103) |
where Bρ is the beam rigidity. A quadrupole is n = 1, a sextupole is n = 2, and so on.
The relationship between the pole tip field and KnL is
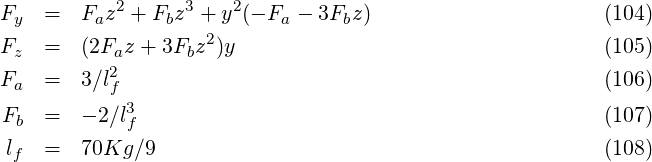 | (104) |
where r is the bore radius.
NIBEND