Zero-length Multipole RF DeFlector from dipole to decapole
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no
| Parameter Name | Units | Type | Default | Description |
| FACTOR | double | 1 | A factor by which to multiply all components. |
|
| TILT | RAD | double | 0.0 | rotation about longitudinal axis |
| A1 | V∕m | double | 0.0 | Vertically-deflecting dipole |
| A2 | V∕m2 | double | 0.0 | Skew quadrupole |
| A3 | V∕m3 | double | 0.0 | Skew sextupole |
| A4 | V∕m4 | double | 0.0 | Skew octupole |
| A5 | V∕m5 | double | 0.0 | Skew decapole |
| B1 | V∕m | double | 0.0 | Horizontally-deflecting dipole |
| B2 | V∕m2 | double | 0.0 | Normal quadrupole |
| B3 | V∕m3 | double | 0.0 | Normal sextupole |
| B4 | V∕m4 | double | 0.0 | Normal octupole |
| B5 | V∕m5 | double | 0.0 | Normal decapole |
| FREQUENCY1 | HZ | double | 2856000000 | Dipole frequency |
| FREQUENCY2 | HZ | double | 2856000000 | Quadrupole frequency |
| FREQUENCY3 | HZ | double | 2856000000 | Sextupole frequency |
| FREQUENCY4 | HZ | double | 2856000000 | Octupole frequency |
| FREQUENCY5 | HZ | double | 2856000000 | Decapole frequency |
| PHASE1 | HZ | double | 0.0 | Dipole phase |
| PHASE2 | HZ | double | 0.0 | Quadrupole phase |
| PHASE3 | HZ | double | 0.0 | Sextupole phase |
| PHASE4 | HZ | double | 0.0 | Octupole phase |
| PHASE5 | HZ | double | 0.0 | Decapole phase |
| PHASE_REFERENCE | long | 0 | phase reference number (to link with other time-dependent elements) |
|
| START_PASS | long | -1 | If non-negative, pass on which to start modeling cavity. |
|
| END_PASS | long | -1 | If non-negative, pass on which to end modeling cavity. |
|
| START_PID | long | -1 | If non-negative, lowest particle ID to which deflection is applied. |
|
MRFDF continued
Zero-length Multipole RF DeFlector from dipole to decapole
| Parameter Name | Units | Type | Default | Description |
| END_PID | long | -1 | If non-negative, highest particle ID to which deflection is applied. |
|
| GROUP | string | NULL | Optionally used to assign an element to a group, with a user-defined name. Group names will appear in the parameter output file in the column ElementGroup |
|
This element simulates an rf deflector with specified multipole content.
Assuming for simplicity that y = 0, the momentum change in the horizontal plane is
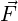 | (101) |
where k = ω∕c and px = βxγ. The deflection is
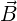 | (102) |
where the approximation results from the fact that pz = βzγ also changes in order to satisfy Maxwell’s equations.
MULT