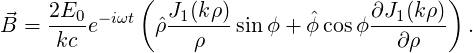10.92 RFMODE—A simulation of a beam-driven TM monopole mode of an RF cavity.
A simulation of a beam-driven TM monopole mode of an RF cavity.
Parallel capable? : yes
GPU capable? : no
Back-tracking capable? : no
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| RA | Ohm | double | 0.0 | shunt impedance, Ra=V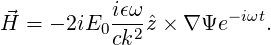 /P /P |
|
|
|
|
|
| RS | Ohm | double | 0.0 | shunt impedance (Rs=Ra/2) |
|
|
|
|
|
| Q | | double | 0.0 | cavity Q |
|
|
|
|
|
| FREQ | Hz | double | 0.0 | Resonant frequency of the
cavity mode |
|
|
|
|
|
| CHARGE | C | double | 0.0 | Deprecated—use CHARGE
element) |
|
|
|
|
|
| INITIAL_V | V | double | 0.0 | initial beam-loading voltage |
|
|
|
|
|
| INITIAL_PHASE | RAD | double | 0.0 | initial beam-loading phase |
|
|
|
|
|
| INITIAL_T | S | double | 0.0 | time at which INITIAL_V and
INITIAL_PHASE held |
|
|
|
|
|
| BETA | | double | 0.0 | normalized load impedance |
|
|
|
|
|
| BIN_SIZE | S | double | 0.0 | bin size for current histogram |
|
|
|
|
|
| N_BINS | | long | 20 | number of bins for current
histogram |
|
|
|
|
|
| INTERPOLATE | | long | 0 | if non-zero, interpolate voltage
within bins |
|
|
|
|
|
| PRELOAD | | long | 0 | preload cavity with
steady-state field |
|
|
|
|
|
| PRELOAD_CHARGE | C | double | 0.0 | beam charge used for
preloading calculations |
|
|
|
|
|
| PRELOAD_FACTOR | | double | 1 | multiply preloaded field by
this value |
|
|
|
|
|
| PRELOAD_HARMONIC | | long | 0 | If detuning
from harmonic is greater than
half the revolution frequency,
automatic determination of
the rf harmonic will fail. Give
the harmonic explicitly with
this parameter. |
|
|
|
|
|
| RIGID_UNTIL_PASS | | long | 0 | don’t affect the beam until this
pass |
|
|
|
|
|
| DETUNED_UNTIL_PASS | | long | 0 | cavity is completely detuned
until this pass |
|
|
|
|
|
| |
A simulation of a beam-driven TM monopole mode of an RF cavity.
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| SAMPLE_INTERVAL | | long | 1 | passes between samples to
RECORD file |
|
|
|
|
|
| FLUSH_INTERVAL | | long | 1000 | samples between flushing
output to RECORD file |
|
|
|
|
|
| RECORD | | STRING | NULL | output file for cavity fields |
|
|
|
|
|
| SINGLE_PASS | | long | 0 | if nonzero, don’t accumulate
field from pass to pass |
|
|
|
|
|
| PASS_INTERVAL | | long | 1 | interval in passes at which
to apply PASS_INTERVAL
times the field (may increase
speed) |
|
|
|
|
|
| FREQ_WAVEFORM | | STRING | NULL | <filename>=<x>+<y>
form specification of input file
giving frequency/f0 vs time,
where f0 is the frequency given
with the FREQ parameter |
|
|
|
|
|
| Q_WAVEFORM | | STRING | NULL | <filename>=<x>+<y> form
specification of input
file giving qualityFactor/Q0
vs time, where Q0 is the
quality factor given the the Q
parameter. |
|
|
|
|
|
| RAMP_PASSES | | long | 0 | Number of passes over
which to linearly ramp up the
impedance to full strength. |
|
|
|
|
|
| BINLESS | | long | 0 | If nonzero, use algorithm that
doesn’t
requiring binning. Best for few
particles, widely spaced. |
|
|
|
|
|
| RESET_FOR_EACH_STEP | | long | 1 | If nonzero, voltage and phase
are reset for each simulation
step. |
|
|
|
|
|
| LONG_RANGE_ONLY | | long | 0 | If nonzero, induced voltage
from present turn does not
affect bunch. Results are not
self-consistent! |
|
|
|
|
|
| |
A simulation of a beam-driven TM monopole mode of an RF cavity.
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| ALLOW_UNBINNED_PARTICLES | | long | 0 | If nonzero, will keep running
even if some particles fall
outside the binning region.
Use with caution! |
|
|
|
|
|
| N_CAVITIES | | long | 1 | effect is multiplied
by this number, simulating N
identical cavities |
|
|
|
|
|
| BUNCHED_BEAM_MODE | | long | 1 | If 1, then do calculations
bunch-by-bunch. If >1, use
pseudo bunches. |
|
|
|
|
|
| BUNCH_INTERVAL | S | double | 0.0 | For pseudo-bunch mode, time
between bunches. |
|
|
|
|
|
| DRIVE_FREQUENCY | Hz | double | 0.0 | drive frequency from
generator. If zero, no generator
voltage is applied. |
|
|
|
|
|
| V_SETPOINT | V | double | 0.0 | setpoint for total cavity
voltage |
|
|
|
|
|
| PHASE_SETPOINT | DEG | double | 0.0 | setpoint for total cavity phase |
|
|
|
|
|
| UPDATE_INTERVAL | | long | 1 | update interval of feedback in
units of rf period |
|
|
|
|
|
| READ_OFFSET | | long | 0 | Offset in buckets of point at
which voltage and phase are
read for feedback relative to
the first bunch passage. A
positive value corresponds to
reading before bunch passage. |
|
|
|
|
|
| ADJUSTMENT_START | | long | 0 | Pass on
which to begin adjustment of
the effective voltage setpoint. |
|
|
|
|
|
| ADJUSTMENT_END | | long | 0 | Pass
on which to stop adjustment of
the effective voltage setpoint. |
|
|
|
|
|
| ADJUSTMENT_INTERVAL | | long | 100 | Interval in passes between
adjustment of the effective
voltage setpoint. |
|
|
|
|
|
| |
A simulation of a beam-driven TM monopole mode of an RF cavity.
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| ADJUSTMENT_FRACTION | | double | 0.0 | Fraction
of voltage setpoint error taken
out on each adjustment step |
|
|
|
|
|
| AMPLITUDE_FILTER | | STRING | NULL | IIR filter specification for
amplitude feedback |
|
|
|
|
|
| PHASE_FILTER | | STRING | NULL | IIR filter specification for
phase feedback |
|
|
|
|
|
| IN_PHASE_FILTER | | STRING | NULL | IIR filter specification for
in-phase component feedback |
|
|
|
|
|
| QUADRATURE_FILTER | | STRING | NULL | IIR filter
specification for quadrature
component feedback |
|
|
|
|
|
| FEEDBACK_RECORD | | STRING | NULL | output file for feedback data |
|
|
|
|
|
| MUTE_GENERATOR | | long | -1 | If nonnegative, gives
the pass on which to mute the
generator. This simulates an rf
trip. |
|
|
|
|
|
| GENERATOR_FACTOR | | double | 1 | Multiplies the generator
current by the specified factor. |
|
|
|
|
|
| NOISE_ALPHA_GEN | | STRING | NULL | <filename>=<x>+<y>
specifying alpha(t) for
generator noise. |
|
|
|
|
|
| NOISE_PHI_GEN | | STRING | NULL | <filename>=<x>+<y>
specifying dphi(t) for
generator noise, in radians. |
|
|
|
|
|
| NOISE_ALPHA_V | | STRING | NULL | <filename>=<x>+<y>
specifying alpha(t) for voltage
noise. |
|
|
|
|
|
| NOISE_PHI_V | | STRING | NULL | <filename>=<x>+<y>
specifying dphi(t) for voltage
noise, in radians. |
|
|
|
|
|
| NOISE_I_GEN | | STRING | NULL | <filename>=<x>+<y>
specifying ni(t) for in-phase
generator noise. |
|
|
|
|
|
| |
A simulation of a beam-driven TM monopole mode of an RF cavity.
|
|
|
|
|
| Parameter Name | Units | Type | Default | Description |
|
|
|
|
|
| NOISE_Q_GEN | | STRING | NULL | <filename>=<x>+<y>
specifying nq(t) for
quadrature generator noise. |
|
|
|
|
|
| NOISE_I_V | | STRING | NULL | <filename>=<x>+<y>
specifying ei(t) for in-phase
voltage noise. |
|
|
|
|
|
| NOISE_Q_V | | STRING | NULL | <filename>=<x>+<y>
specifying eq(t) for quadrature
voltage noise. |
|
|
|
|
|
| GROUP | | string | NULL | Optionally used to assign an
element to a group, with
a user-defined name. Group
names will appear in the
parameter output file in the
column ElementGroup |
|
|
|
|
|
| |
This element simulates a beam-driven monopole mode cavity using the fundamental theorem of beam
loading and phasor rotation. In addition, a generator-driven field may be included using a feedback system
[44].
Note on phase conventions: the phase convention for the PHASE_SETPOINT parameter of RFMODE is the
same as for the PHASE parameter of RFCA. However, in the output files from RFMODE, i.e., the files
requested with the RECORD and FEEDBACK_RECORD parameters, a different convention is used, which differs
by -90 degrees from the PHASE_SETPOINT parameter.
The feedback implementation uses either amplitude and phase feedback or else in-phase and
quadrature feedback. Figure 3 shows the model used for the feedback system. More information is
available in [44].
Rf feedback is active when a non-zero value is given for DRIVE_FREQUENCY and when either
AMPLITUDE_FILTER and PHASE_FILTER or else IN_PHASE_FILTER and QUADRATURE_FILTER are given.
These parameters name SDDS files that define filters in the z domain
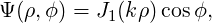 | (144) |
which translates into the discrete time domain as
![1 ∑r 1 ∑m
y[n] = ---- aiyr-i + --- bixn- i,
a0 i=1 a0i=0](elegant190x.png) | (145) |
where y[n] is the filter output (e.g., additional generator current) and x[n] is the filter input (e.g., the
voltage error signal). The filter files must each contain two columns:
- denominator — The ai filter coefficients. These should generally sum to zero or nearly zero.
- numerator — The bi filter coefficients. These are generally very small.
Each file can consist of up to four pages, with each page representing one filter in a parallel filter bank formed
from all pages. The output of the four stages is added to obtain the control signal. The number of rows in
the page is given by the larger of r or m; in the case of multiple pages, the number of rows in each page is
given by the largest r or m from the highest order filter amongst the pages, by simply stuffing the rows of
the other pages with zeros, i.e., rows representing orders of z down to z-l where l is the largest r or m of
the filter pages.
For example, a digital low-pass filter with DC gain of k can be specified as
![y[1] = e-pT y[0]+ k (1 - e-pT)x[0],](elegant191x.png) | (146) |
where p is the frequency of the pole and T is the sample interval.
The feedback loop reads the cavity state and acts on the generator at a fixed interval (in buckets) of
UPDATE_INTERVAL. The timing of this activity is aligned to the arrival time of the first bunch in the
RFMODE element. By default (READ_OFFSET=0), the timing is such that the state is read just before the
next arrival of that bunch; in particular, it is 180 degrees ahead of that arrival. If bunches are
equally spaced by, say Nb buckets, the UPDATE_INTERVAL parameter should ideally be mNb,
where m > 0 is an integer. This ensures that the state is read at a fixed timing relative to the
bunches.
The rf feedback feature makes use of the voltage amplitude measured when there is no bunch present.
The RECORD file shows the voltage seen by the beam, computed by averaging over the voltage for each
particle. These may deviate by values from a few percent to of order ten percent, depending on the loss
factor for the cavity and the number of bunchess; this is caused by the fact that the rate at which an
intense bunch removes energy from the cavity will typically, albeit briefly, exceed the power from
the generator. To reduce the impact of this effect, one may use the ADJUSTMENT_FRACTION,
ADJUSTMENT_START, and ADJUSTMENT_INTERVAL parameters to modify the voltage setpoint. If
ADJUSTMENT_FRACTION is non-zero, then for every ADJUSTMENT_INTERVALth pass after the
ADJUSTMENT_STARTth pass, the voltage setpoint will be adjusted based on a comparison of the
bunch-averaged voltage to the user’s setpoint. E.g., if the bunch-averaged voltage is 100 V too low and
ADJUSTMENT_FRACTION is 0.1, the voltage setpoint will be raised by 10 V. Users should note that if
ADJUSTMENT_FRACTION is too large or ADJUSTMENT_INTERVAL is too small, the system may be
unstable.
Normally, the field dumped in the cavity by one particle affects trailing particles in the same turn.
However, if one is also using a WAKE or ZLONGIT element to simulate the short-range wake of the cavity,
this would be double-counting. In that case, one can use LONG_RANGE_ONLY=1 to suppress the same-turn
effects of the RFMODE element.
Two output files are available: the RECORD file includes bunch-by-bunch data on the beam-induced
fields and the total cavity fields. The FEEDBACK_RECORD file includes tick-by-tick data from the feedback
system simulation; writing this file this can significantly degrade performance.
NB: when BUNCHED_BEAM_MODE is set to a value other than 1, in order to obtain the effect of several
bunches while tracking only one bunch, the total charge set with the TOTAL parameter of the
CHARGE element should equal the charge in a single bunch, not the entire beam. However, when
BUNCHED_BEAM_MODE=1 (allowing an indeterminant number of bunches to be actually present), then TOTAL
should be the total for all bunches together.
Explanation of <filename>=<x>+<y> format: Several elements in elegant make
use of data from external files to provide input waveforms. The external files are SDDS files,
which may have many columns. In order to provide a convenient way to specify both the
filename and the columns to use, we frequently employ <filename>=<x>+<y> format for the
parameter value. For example, if the parameter value is waveform.sdds=t+A, then it means
that columns t and A will be taken from file waveform.sdds. The first column is always the
independent variable (e.g., time, position, or frequency), while the second column is the dependent
quantity.
 /P
/P
![1 ∑r 1 ∑m
y[n] = ---- aiyr-i + --- bixn- i,
a0 i=1 a0i=0](elegant190x.png)
![y[1] = e-pT y[0]+ k (1 - e-pT)x[0],](elegant191x.png)